Calculating the exact position of any Pole of Inaccessibility is fraught with difficulty as all countries or Islands are irregular-shaped 3D objects.  When you are looking at a land mass, for example, how far do you assume the sea to come into a river estuary?  What position on a beach should you place the sea when considering tides? Should the PIA be recalculated every time there is a rockfall due to coastal erosion? And over-sitting all of this is the fact that any country or island sits on a sphere.  In the case of the Northern and Southern-most PIAs, where does the ice sheet stretch to? 

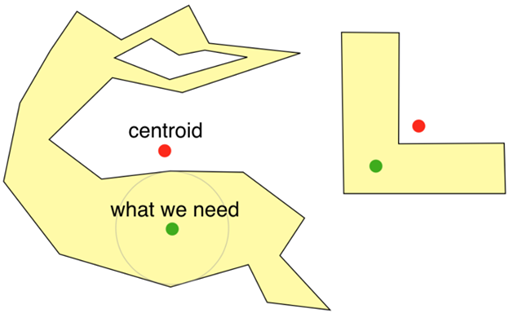
Centre of Gravity

Once the extent of the land mass has been determined, the generally accepted method to locate the centre of an island, country or state, according to the majority of mapping organisations including NASA, is the Gravitational Method: finding the Centre of Gravity of the land mass. Imagine drawing the country or island on a piece of card, cutting it out with scissors and then balancing the cut-out on a pin-head. 

Of course, this then beggars the question as to whether you should use a 3D or 2D model to calculate the CoG.  In other words, do you give more ‘weight’ to mountainous regions.  But since the height of mountains doesn’t make a point closer to the centre, the 2D calculation is preferred.

In mathematics, this 2D CoG is termed the Centroid of the Plane Figure (the cut-out) which is the arithmetic mean position of all points in that figure.

Calculating Poles of Inaccessibility

You’ll remember, though, that locating Poles of Inaccessibility are very different from finding the centroid of something.

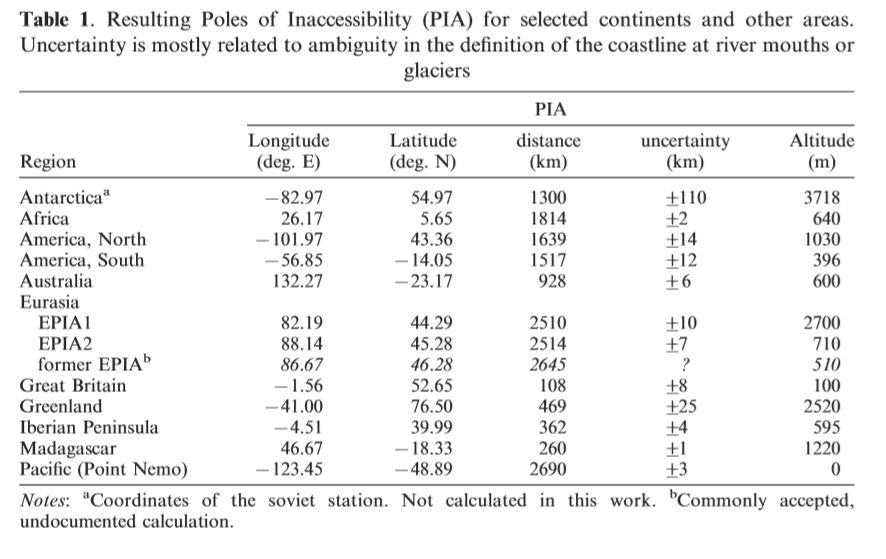
An algorithm for calculating the PIAs was presented in the Scottish Geographical Journal Volume 123, September 2007, issue 3 by Daniel Garcia-Castellanos and Umberto Lombardo Pages 227-233) which used an iterative method to ‘test’ candidate points for the PIAs. They tested approximately 80,000 points to locate one PIA. See here for more details.

This was the first study to use computational power, geographical databases and ‘digital coastlines’ to calculate the poles. Only graphical methods had been used previously (essentially drawing the biggest circle you could on a land mass map).

Their paper presented PIAs for six of the The Eight Poles – excluding Antarctica but including two candidates for Eurasia – Great Britain, Greenland, the Iberian Peninsula, Madagascar and Point Nemo.

Calculating Points of Inaccessibility

In 2019, Chris Brown commissioned Miso to calculate several Points of Inaccessibility  to enable a series of personal expeditions.

This is how the Points of Inaccessibility were calculated.

• The polygon of the desired geographical area was created using ESRI ArcMap.
• Using the QGIS plugin “Pole of Inaccessibility”, the Miso team identified the point which sat the furthest distance from any border within a polygon’s area.
• The plugin calculates the Point of Inaccessibility for the given polygon, using the polylabel algorithm*, as implemented in the QGIS core code.
• In the Pole of Inaccessibility plugin, the team selected the required polygon as the input layer, and set the tolerance to 0.000001.
• Chris and the team then wanted to see where the point was geographically positioned, and so used the “quick map services” plugin to open the Google Roads base map.
• Next, they exported the point as a *.shp file.
• In FME, Miso created a workspace which attributed Latitude and Longitude co-ordinates to the point created using QGIS.
• A second workspace was created to measure the distance from the point to the nearest boundary in the polygon. This workspace hinged on the inclusion of the “GeographicNeighborFinder” transformer, which finds the closest candidate feature within a specified maximum distance of each Base feature.

*The Polylabel algorithm is iterative in nature, similar to the Garcia-Castellanos method. It calculates and locates the most distant internal point from the polygon outline (land mass boundary).  However, it differs from the 2007 algo in that it guarantees finding a global optimum within the given precision and is around 10 to 40 times faster. 

More technical notes on the polylabel algorithm used in QGIS by Miso, are available here: https://github.com/mapbox/polylabel